Quelques notions de mécanique

Pour bien comprendre le mécanisme d'effondrement des tours du WTC, quelques notions de base sont nécessaires.

Mais n'ayez crainte, les explications seront aussi imagées que possible pour bien comprendre le phénomène physique sous-jacent.

Le flambement des éléments comprimés

Le terme de flambement (ou parfois flambage, les deux sont utilisés) désigne un phénomène bien connu des ingénieurs, que ce soit en mécanique ou en bâtiment, mais qui n'a rien à voir avec le feu !! Le flambement est une instabilité très dangereuse qui peut apparaître pour les éléments élancés.

EXPLICATION :

Pour présenter ce phénomène, j'ai réalisé une petite image avec différents éléments...

A gauche sur la figure, 3 objets :   * une masse en granit * un cylindre de bois de hauteur égale à 2 fois son diamètre * un cylindre de bois de hauteur égale à 100 fois son diamètre   (peu importe en fait le type de matériaux)     L'expérience consiste à poser successivement la masse en granit sur les deux cylindres. Ces éléments sont alors soumis à un effort de compression.   L'expérience montre que la masse ne reste pas en équilibre sur le deuxième cylindre : celui-ci fléchit et la masse tombe.   C'est cet état instable qui est appelé le flambement (ou flambage) d'un élément.

Chacun peut faire une expérience de flambement chez lui : il suffit de prendre une règle d'écolier plate de 30 cm en plastique et de la comprimer entre ses deux mains. A partir d'une certaine pression exercée sur la règle, on sent que celle-ci sort de son plan et n'a pratiquement plus de résistance.... Vous avez atteint là la force critique.

Il est évident que c'est le rapport entre la hauteur et la section du cylindre qui va être important pour caractériser cette instabilité. C'est ce qui est appelé l'élancement.

Mathématiquement, l'élancement (lambda) est défini à partir de la section de l'élément (A), son inertie (I) et sa longueur (L) :

Il est alors possible de calculer de manière purement théorique la force maximale applicable sur l'élément avant l'apparition de cette instabilité. C'est la force critique d'Euler

Dans le cas suivant où la poutre est tenue à ses deux extrémités par une articulation, la force critique est donnée par la formule :   :   E étant le module d’Young du matériau (rigidité).

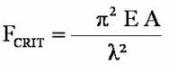Un cas d'étude en laboratoire de recherche.		Des rails SNCF en 2003 lors de la canicule : quelques dizaines de degrés ont suffi pour mettre les rails en flambement. Normalement, ce genre de problème est évité grâce à des joints de dilatation.

En théorie lorsque cette instabilité est atteinte, plus rien n'empêche l'élément de se déformer et donc de se rompre.

Dans la pratique, sous certaines conditions (d'appui notamment), il est possible d'aller au delà mais guère plus.

Il faut souligner également que les calculs de la force critique d'Euler se font en faisant l'hypothèse d'un élément parfaitement rectiligne. Si à la fabrication, les éléments n'ont pas une rectitude parfaite, la force limite avant flambement est réduite.

Cette instabilité est TRES dangereuse car la rupture peut arriver très vite et c'est un peu le cauchemar de tout concepteur en bâtiment. Dans les nouveaux règlements de calculs européens (appelés Eurocodes) ce phénomène est bien sûr pris en compte. Pour les cas les plus défavorables (grands élancements), des coefficients correcteurs font que les ingénieurs ne prennent en compte que 10 à 20 % de la résistance réelle du matériau.

IMPORTANT :

D'après la formule donnant la force critique, la résistance au flambement d'un élément est directement proportionnelle au module d'Young du matériau (E). Cela veut dire que si ce module est réduit de 80 %, la force critique avant flambement est aussi réduite de 80 %...

Or, nous le verrons lorsque nous parlerons de l'acier, quand sa température approche les 800°C, son module a perdu 90 % de sa valeur ! Cela veut dire que si un poteau en acier atteint cette température, sa capacité portante vis à vis du flambement sera divisée par 10...

Bien sûr, nous y reviendrons...

Les effets dynamiques sur une structure

Les sollicitations dynamiques sur une structure peuvent être diverses et engendrer des réponses tout aussi différentes. J'en présenterai ici deux : les sollicitations cycliques et les chocs.

Les actions variables dans le temps, et plus particulièrement les sollicitations cycliques, peuvent engendrer des oscillations très importantes dans une structure.

Deux exemples célèbres : le pont de Tacoma (Etats-Unis) et le Millenium Bridge à Londres, encore en service mais muni aujourd'hui "d'amortisseurs"...

Ce phénomène (qui est appelé "résonnance") est dû à des forces qui varient de façon régulière et répétitive ("actions périodiques") et qui agissent en concordance ("en phase") avec les oscillations de l'édifice. Cela a pour effet d'accroître l'amplitude de ces oscillations à chaque pas de temps, parfois jusqu'à la rupture.

Ce n'est pas le phénomène mis en jeu dans l'effondrement des tours du WTC, mais ces exemples spectaculaires montrent que des charges même faibles (vent pour le pont de Tacoma, piétons pour la passerelle) peuvent parfois avoir des conséquences désastreuses.

Pour les chocs, chacun comprend bien le phénomène, pas besoin d'explication bien longue...

Supposons qu'un élément en mouvement vienne heurter une structure. L'énergie cinétique du corps en mouvement (la même qui fait que votre voiture avance encore lorsque vous arrêtez d'accélérer) est alors transmise lors du choc à la structure immobile. Les deux éléments vont bien sûr fortement se déformer, il n'y a qu'à voir les résultats de la collision de deux véhicules.

Deux cas se présentent alors pour la structure percutée :

* soit le matériau est capable de se déformer suffisamment (sans rompre) pour absorber l'énergie transmise et il peut revenir dans sa position initiale (l'énergie élastique a été mobilisée), voire rester légèrement déformé (énergie plastique, non réversible),

* soit il n'est pas capable d'absorber cette énergie et il se rompt.

C'est ce qui fait que vous pouvez monter sur le pare-brise de votre voiture et appliquer tout votre poids (charge statique) mais qu'un tout petit gravillon de seulement quelques grammes mais en mouvement peut le fendre (choc ou action dynamique). L'énergie cinétique du gravillon engendre une telle concentration de contraintes sur la pare-brise que le matériau se casse.